Небесная сфера

 

Продолжим нашу аналогию между навигационными и астроно­мическими методами определения места. Если в навигации для опре­деления места судна по пеленгам нам надо прежде всего знать поло­жение маяка (на Земле), то в астрономии нам надо знать положение светила (на небе). Разница лишь в том, что маяки на Земле занимают неизменное положение, светила же                       

на небе меняют свое положение по отношению к неподвижному  наблюдателю благодаря суточному

движению небесного свода, Задача определения места светила  на небе упрощается и облегчается

введением понятия вспомогательной  сферы, так называемой  небесной сферы.

Если  внимательно всматриваться в небо,  то нетрудно заметить, что хотя светила и меняют свое положение по отношению к наблюдателю (восходят, достигают предельной высоты и затем заходят), но взаимное угловое положение их между собой остается неизменным. Фактическое расстояние от Земли до каждого отдельно взятого светила весьма различно: бли­жайшее — Луна — находится от нас на расстоянии 360 тыс. км, Солнце — 150 млн. км, а звезды на расстоянии многих миллиардов километров. Но величина угла между светилами, измеренного из центра Земли, не зависит от расстояний. Это обстоятельство поз­воляет нам построить в своем воображении небесную сферу, которая даст возможность с геометрической точки зрения совершенно точно  определять положение любого светила для любого заданного момента и для любого наблюдателя, где бы он на Земле ни находился.

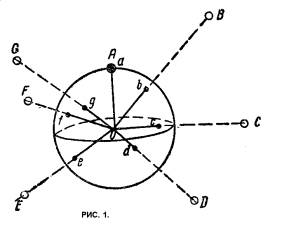
В самом деле, вообразим себе произвольной величины шар (сферу), описанный из центра Земли (рис. 1). Пусть А, В, С, D, Е, F, О представляют положение небесных светил в мировом пространстве.

Соединив их прямыми линиями ОА, 0В, ОС, OD и т. д. с центром сферы, получим в пересечении этих прямых с поверхностью сферы в точках а, b, с, d и т. д. проекции светил на сфере.

На рисунке видно что относительное расположение проекций светил на сфере будет точно такое же, как в мировом пространстве, так как углы между ними, измеренные из центра сферы, остались теми же. Это позволяет при решении задач учитывать не действительное место­положение звезд, а лишь их проекции на сферу произвольного радиуса.

Таким образом, небесной сферой называется сфера произволь­ного радиуса с нанесенными на ней проекциями небесных светил,, Небесная сфера является геометрическим изображением видимого нами небесного свода. Чтобы можно было на этой сфере определять положение светил, необходимо построить на ней сетку линий и кругов, аналогичную той, которую мы применяем на Земле для определения географических координат. 

Продолжим ось вращения Земли (рис. 1а) до пересечения с поверхностью небесной сферы. Получим линию P’_N P’_S , которую будем называть осью мира, а точки P_N и Ps — 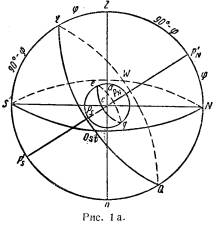полюсами. Они представят собой проекции полюсов Земли на небесную сферу.

Большой круг EQ, плоскость которого перпендикулярна оси, называется небесным экватором.                   

Небесный экватор представляет собой проекцию земного        экватора на небесную сферу.Проведем через место наблюдателя (точка а) отвесную линию (Рис. la.)  Zn и продолжим ее до пересечения с поверхностью небесной сферы. Пересечение отвесной линии со сферой дает точку зенита Z ;

и надира п. Точка Z является проекцией места наблюдателя, нахо­дящегося в точке а.                                            

Большой круг NOSW, плоскость которого перпендикулярна отвесной линии, называется истинным горизонтом.   Большой круг небесной сферы NP’_N ZESP’_SnQ ,проходящий через  полюсы мира и точки зенита и надира, называется меридианом наблюдателя.                                                

Меридиан наблюдателя является проекцией земного меридиана наблюдателя, находящегося в точке а, на небесную сферу. Пересечение истинного горизонта с меридианом наблюдателя дает  точки N (Nord) и S (Sud). Плоскостью истинного горизонта небесный  экватор делится на две равные части. Точки пересечения экватора  с истинным горизонтом дают точки О (Ost) и W (West).

Плоскость экватора делит небесную сферу на два полушария:

северное EZP'_NNQ и южное ESP'_S nQ. Плоскость истинного горизонта делит небесную сферу на две равные части: надгоризонтную NP'_NZES и подгоризонтную NQnP’_SS.

Полюс мира p’n, находящийся в надгоризонтной части сферы, называется повышенным полюсом, P’s в подгоризонтной части — пониженным полюсом. На рис. 1а видно следующее: место наблюдателя, определяемое точкой и, располагается в северном полушарии, и p'n является повы­шенным полюсом. Отсюда следует, что наименование повышенного полюса всегда будет соответствовать наименованию широты места наблюдателя. Если бы место наблюдателя располага­лось в южной широте, то в надгоризонтной  части сферы располагался бы Ps.

Ось мира Р’_NР’_S делит ме­ридиан наблюдателя на две рав­ные части: полуденную P'_NZESP's, располагающуюся от повышенного полюса через зенит к пониженному, и полуночную P’_NNQnP’s,— от повышенного по­люса через надир к понижен­ному.

Дуга меридиана наблюда­теля np'_N, заключенная между истинным горизонтом и повы­шенным полюсом, называется географической широтой места наблюдателя. Нетрудно убедиться (рис. 1а), что дуга земного меридиана еа, равная широте места наблюдателя, находящегося в точке а, и дуга меридиана наблюдателя EZ измеряются одним  и тем же центральным углом. Следовательно,  дуга   Е Z также соответствует широте места наблюдателя. На осно­вании изложенного, обозна­чив широту буквою у, можем написать:

j = ea =EZ = NP’_N = SP’_S = nQ

Дуги ZP’_N = ES = nP’s =  qn  =90° —j   называются дополнением широты.

Широта измеряется от 0 до 90° к N и S.